BUAA面向对象迭代开发总结-表达式化简
BUAA面向对象迭代开发总结-表达式化简
shiki面向对象迭代开发总结-表达式化简
设计思路
在本次项目中,需要实现一个能够处理自定义普通函数,自定义递推函数,三角函数,导数表达式的表达式去括号程序。
各个设定的形式化表述如下(各项之间可存在空白符)
Exper = [+/-]Exper +/- Term
Term = [+/-]Term * Factor
Factor -> Var | Num | SubExpr | Dao(导数表达式) | Func(递推函数) | NormalFunc(普通函数)
Var = (x|y)^n
Num -> 整数
Dao = dx(Expr)
Func = f{k}(Factor,Factor) //可不含第二个Factor
NormalFunc = g(Factor,Factor)|h(Factor,Factor) //可不含第二个Factor
SubExpr = ([+/-]SubExpr +/- SubTerm)^n整体思路如下:
词法分析将输入的字符串解析为Token列表。
递归下降解析Token列表构建表达式树,同时将自定义函数展开为表达式。
递归地展开表达式中的括号得到一个广义Poly列表,同时为了利于计算将Term之间的,SubTerm之间的符号放入Poly中。其中广义Poly定义如下:
\[ Poly = a*x^b*\prod sin(Poly)^{k_i}*\prod cos(Poly)^{m_i} \]化简上一步得到的Poly列表并输出。
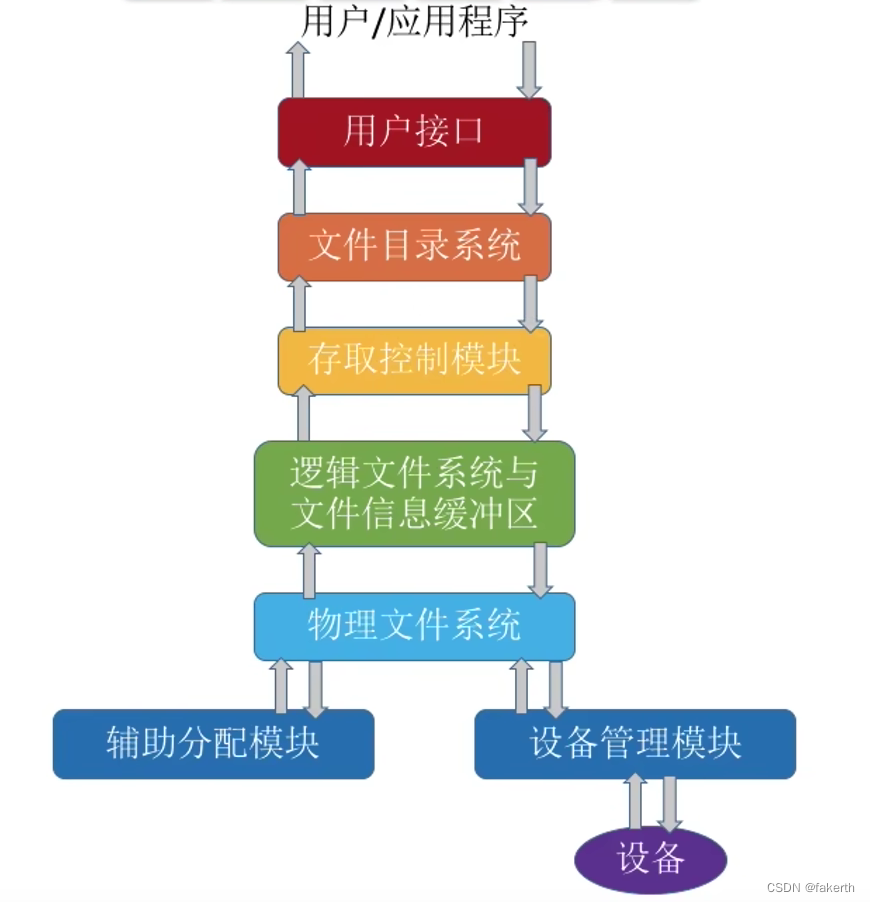
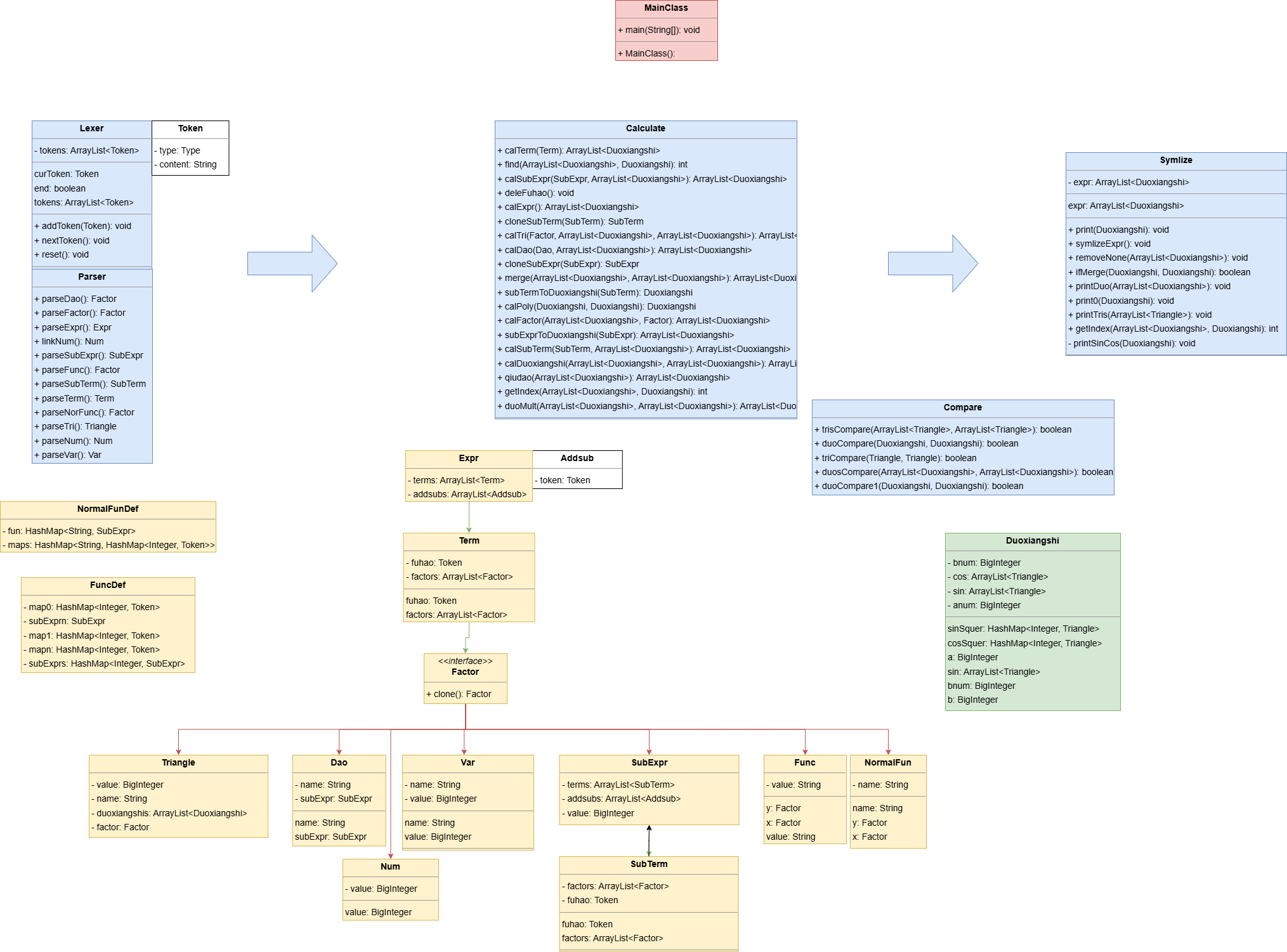
程序结构
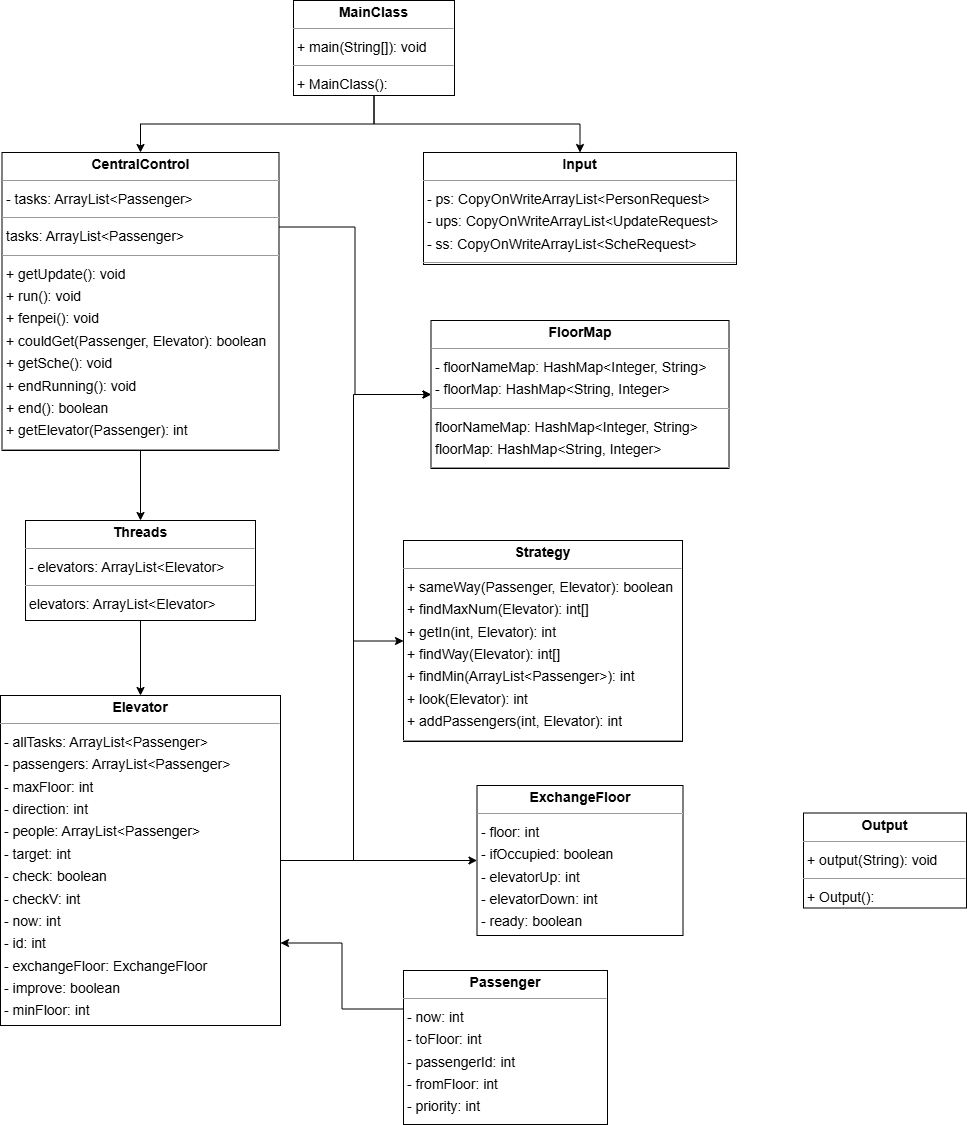
类图如下:
红色方框为主类MainClass
蓝色方框为计算类,词法分析Lexer,递归下降Parser,计算Calculate,比较Compare,化简Symplize
黄色方框为递归下降解析表达式得到的表达式树上的节点类
白色方框为过程中部分属性的类,如Token保存了词法分析得到的元素
绿色方框为储存Poly的类
蓝色箭头表示程序计算顺序
绿色箭头表示形式化表述中描述的层次关系
红色箭头表示继承关系
架构分析与设计体验
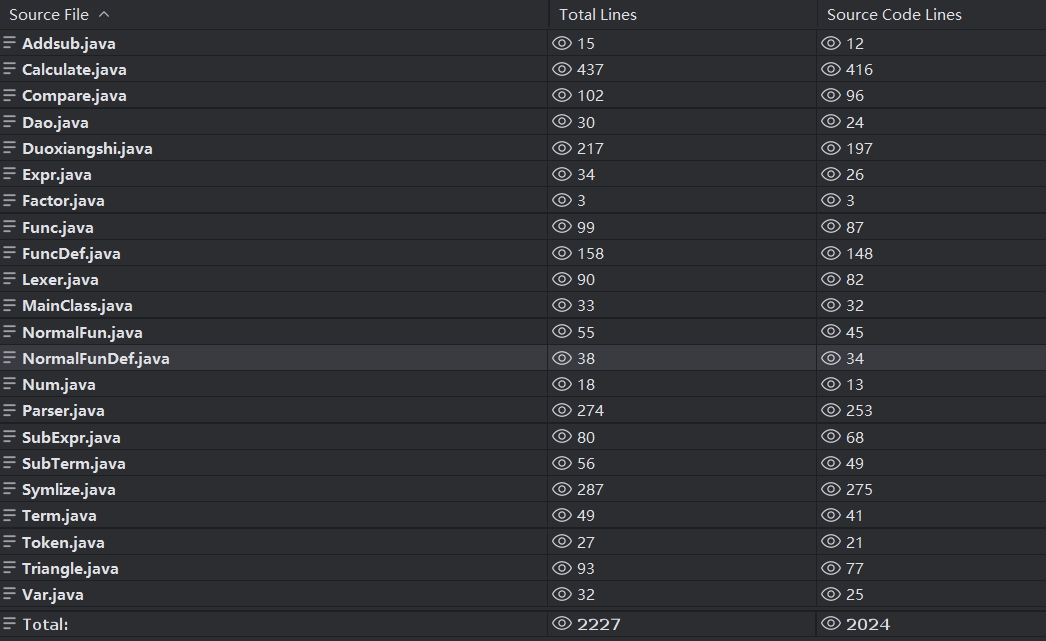
使用IDEA的statistic分析得到代码规模如下:
由此可知,代码规模较大的类有Calculate,Symplize,Duoxiangshi,Parser。这几个类实现了递归下降,表达式计算,化简的大部分代码,代码量较大。
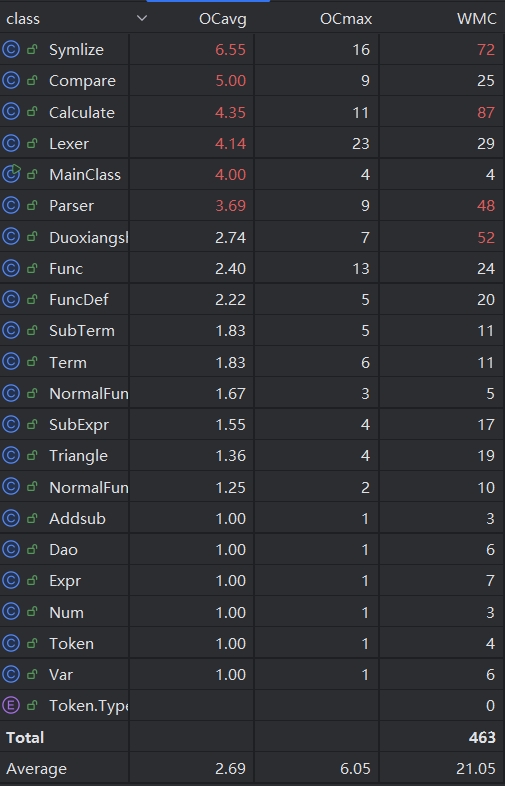
使用IDEA的MetricsReloader插件得到代码复杂性分析如下:
由于表达式计算化简,比较,递归下降过程中涉及到大量的递归调用,以及对不同种类的因子的分别处理产生了大量分支判断,导致这几个部分的代码复杂度较高。
架构优点:
Parser中的方法可以用于自定义函数在定义时的解析,减少重复代码
设计表达式计算,比较,化简类,使代码结构清晰
设计广义多项式类,将后续迭代的新增项转化为广义多项式即可沿用前面迭代的代码,降低增量
架构缺点:
- 解析自定义函数的定义表达式时,为了使用Parser中的方法,写了大量重复代码,还使得Parser类,FuncDef类,Lexer类之间的耦合度升高,增加了debug的难度
- 未在多项式类中实现toString方法以便于输出,在Symplize方法中输出增加了多项式类和化简类的耦合度
设计体验如下:
- 第一次作业中,没有三角函数,自定义函数,求导的影响,我直接设计了多项式类存储变量的系数和指数,较为方便。但是第二次作业加入了自定义递推函数和三角函数,对于三角函数的处理,我拓展了多项式类,采用上述的广义多项式类,对于自定义递推函数,为了贴合广义多项式类,我在递归下降的过程中直接将自定义递推函数进行展开为一棵表达式子树,剩下部分和前面的工作一致,同时,由于新增了三角函数,表达式化简过程中的合并难度比第一次作业提高了不少,故新建了比较类,其中实现了递归的广义多项式比较(即比较变量系数,指数,三角函数列表中的各个三角函数,比较三角函数时又调用自身比较三角函数携带的因子)。第三次作业新增普通自定义函数,求导运算,对于普通自定义函数只需要模仿自定义递推函数的形参实参替换过程在递归下降过程中展开即可,求导运算则在Calculate类中新增导数计算方法,其余工作与先前一致。
- 可能的新迭代情境:增加指数函数。此时在递归下降过程新增对指数函数的解析,在广义多项式类中新增指数函数属性,并为其设计合并和比较方法即可,大多数可在原基础上增加,无需过多重构。
BUG分析
自身BUG
测试中发现的bug:在自定义递推函数的定义解析中,直接调用Parser中的函数导致符号解析出现bug
bug原因:解析自定义函数的定义表达式时,为了使用Parser中的方法,增加了Parser类,FuncDef类,Lexer类之间的耦合度,导致需要重新考虑指向Token列表元素的指针的移动,并由此催生出了bug
查找他人bug的策略
- 使用测评机进行随机测试
- 略读他人代码,观察其是否使用字符串替换,正则表达式匹配等方法并设计针对这几种方法易错点的测试样例
- 针对一些共性的易错点构造样例,如
sin(0)^0等
优化
- 实现了基于恒等式
sin(x)^2+cos(x)^2=1的化简,此优化由于需要进行大量的查找和比较,使代码复杂度上升了,可能的解决方案:采用treemap存储三角函数因子,键设为其携带的多项式,重写比较方法使其能够比较多项式。 - 计算表达式时每展开一个括号则进行合并同类项操作,防止因为嵌套过多括号导致计算幂和乘法时时间复杂度指数级增长,新增merge方法进行合并同类项,需要合并时调用merge方法,可以在一定程度上保持代码简洁。
心得体会
深刻体会开幕雷击,第一次迭代之所以难,就是因为要实现从0到1的突破,上来给我开学第一周干破防了。到了第二次迭代增加了自定义递推函数和三角函数,又是一个难度的飞跃,年级上的强测成绩从0分到100分都有,人数也差不多(什么均匀分布),第三次迭代增加求导和自定义普通函数,难度有所下降。
总而言之,难度设计堪称一坨,开学第一周就给你上强度,第二周的迭代增量多得离谱,第三周难度又降下去了,能不能把难度匀一匀啊。